Vertical Ladders in Pathfinder

We recently had a question about modeling vertical ladders in Pathfinder. This post will describe the details of how to accomplish this. This question came from Saqib Mehmood of Aalborg University in Denmark, who was modeling wind turbine evacuation. Saqib Mehmood was joined on this project by a team including Anders S. Kristensen, Francisco Manuel Dieguez Barreiro, Hana Softic, and Yannan Zhou.

Geometry

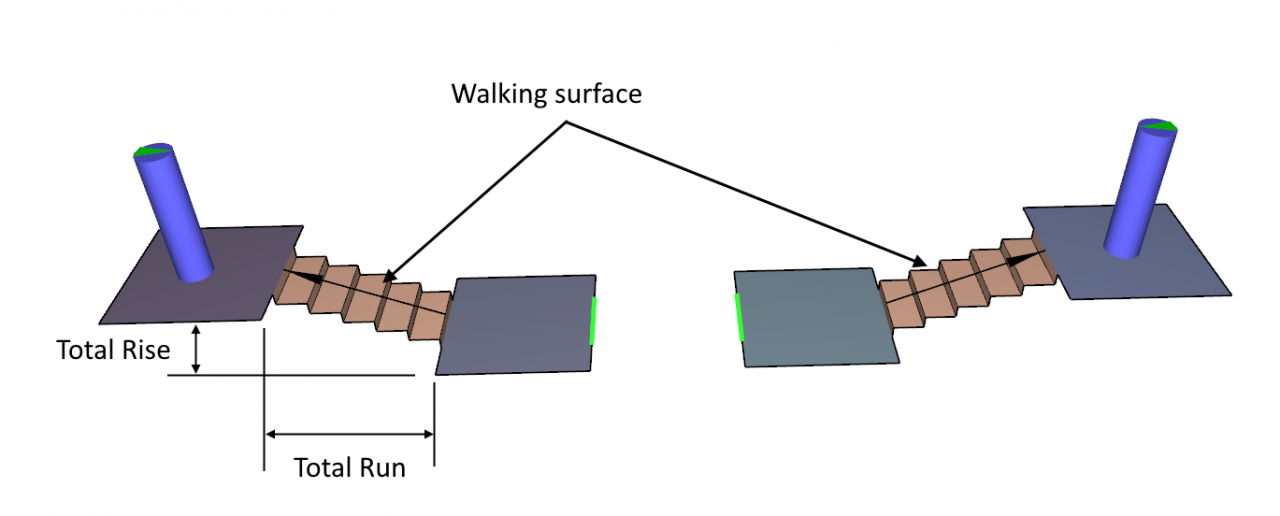
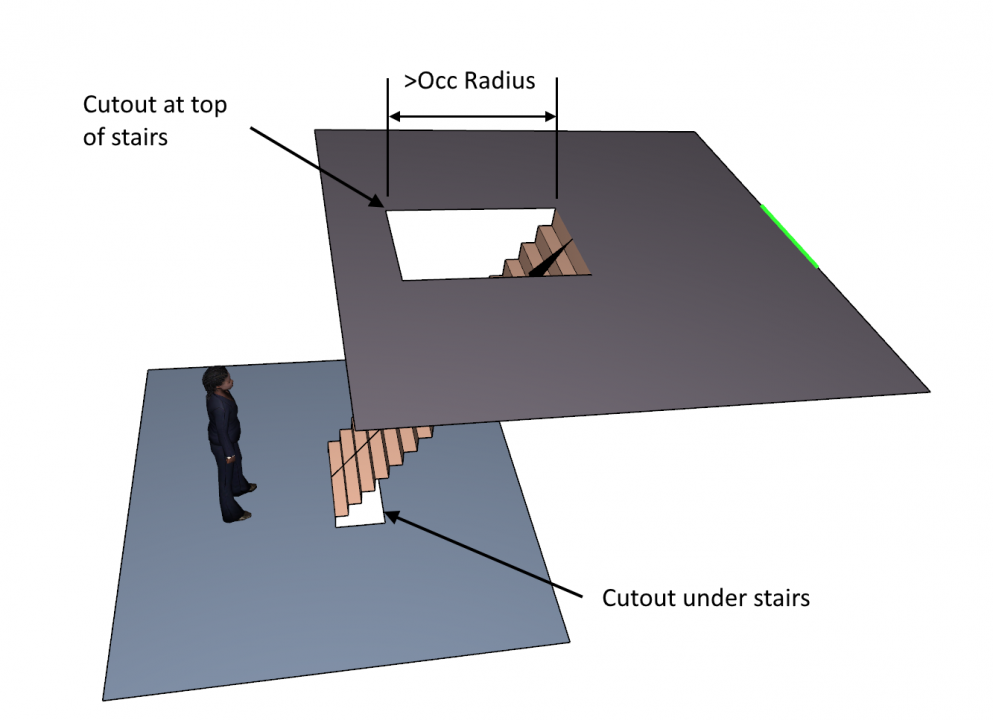
Figure 1 shows normal stairs. Each end of the stairs must connect to boundary edges of the rooms. If the stairs connect the interiors of the rooms, cutouts at the top and bottom must be used, Figure 2. The top cutout must be larger than the occupant radius and stairs cannot be truly vertical, there must be some slope. The walking surface is naturally defined as the top surface of the stairs.

Pathfinder does not have ladders, but ladders can be represented as steep stairs. Figure 3 shows ladders connecting two floors.

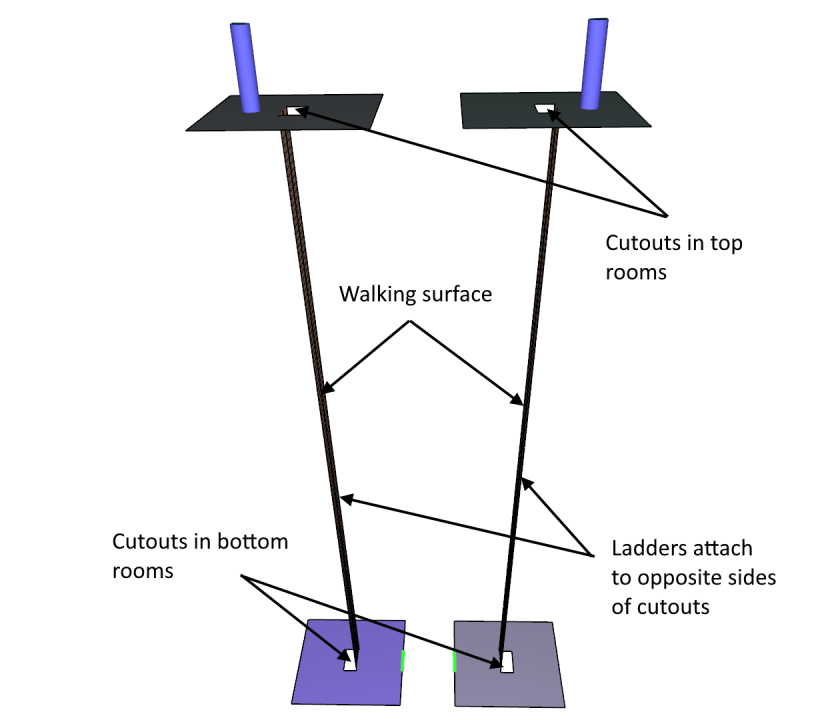
In this model, the distance between floors is 20 m. The cutouts in the top and bottom floors are vertically aligned and measure 1 m by 0.5 m. Because the ladders connect to opposite sides of the holes, there is a slight slope to the ladders. The walking surface of the ladders is the face of the ladder whose normal has a small positive Z component.

Speeds

We want to specify occupant speed on a ladder. By default, Pathfinder modifies the speed on stairs based on the approach described in the SFPE Engineering Guide - Human Behavior in Fire, 2003. These values are not appropriate for a vertical ladder, so we will use a stair speed modifier to obtain the desired value.

As described in the Pathfinder Technical Reference section Path Following in SFPE Mode, the occupant base speed $v_{b}$ is given by:

$$v_{b}=v_{max}\times v_{f}(D)\times v_{ft}$$

Where $v_{max}$ is the occupant's maximum speed entered into the user interface as Speed, $v_{f}(D)$ is the density speed modifier, and $v_{ft}$ is the terrain speed modifier.

The terrain speed modifier $v_{ft}$ is defined as:

$$v_{ft}=\frac{k}{1.4}$$

Where $k=1.4$ is the value for level terrain.

For stairs, the value of $k$ depends on the stair riser and tread that is input in the Pathfinder user interface, Figure 4. Note that $k$ is not calculated using the physical stair geometry, it is calculated based on the user input. For our purposes it is sufficient to know that a stair with a rise of 19.0 cm and a tread of 25.4 cm gives a value $k=1.0$.

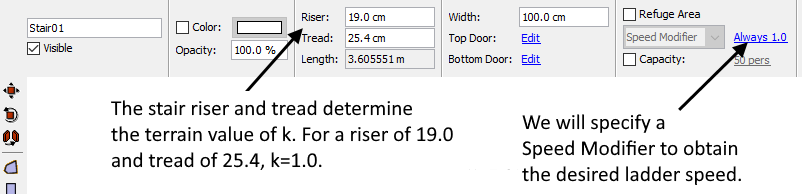
On steep stairs the density is low so the density modifier $v_{f}(D)=1.0$. For a stair with rise of 19.0 cm and tread of 25.4 cm $k=1.0$, so the occupant speed is given by:

$$v_{b}=v_{max}\times \frac{1}{1.4}$$

We can multiply $v_{b}$ by a stair speed modifier to obtain the desired ladder speed.

$$v_{ladder} = \text{modifier} \times v_{b} = \text{modifier} \times \frac{v_{max}}{1.4}$$

By default Pathfinder $v_{max}=1.19\text{m/s}$ and if we desire a ladder speed of 0.25 m/s, then the speed $\text{modifier} = 0.294$.

Example

We run the example using the stair parameters shown in Figure 5. We also select some occupants, click the More button, and enable csv output of individual data.

Figure 6 shows the initial positions of the occupants and Figure 7 shows the occupants descending.

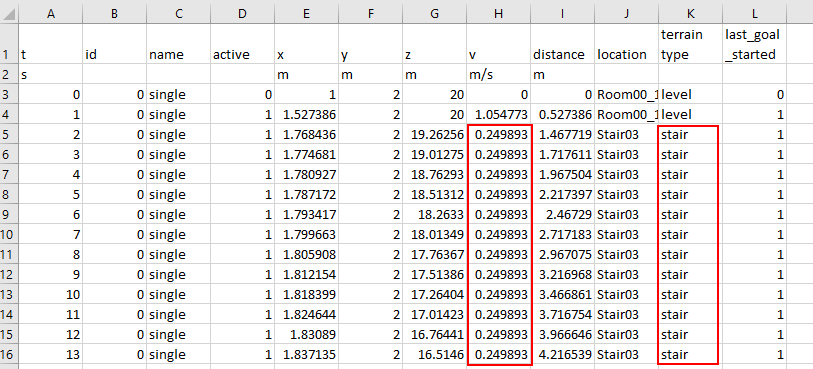
We can open the csv file for the ladder with the single occupant and see that the speed on the ladder is 0.25 m/s. Similar results are obtained for the ladder with multiple occupants, with some initial stop/start movement as they adjust on the ladder.

Additional Comment: In this example, I used the stair speed modifier to control the ladder speed. An alternate approach would be to change the speed/density curve for stairs in the occupant Profile. This has the advantage of allowing a single profile to represent different speeds up and down the ladder. It has the disadvantage that it affects speeds on normal stairs also.

Download File

You can download the Pathfinder model here.

Ladders Post